Introduction

APL is fantastic for working with linear data. If you can organise your data in an array, you have dozens of primitives and years of collective wisdom to lead you to success. Sadly, in the wild, there are many problems which have a fundamentally non-linear structure. These present an issue for the brave APL programmer, whose array primitives struggle to cope.

One of the most common cases of this is dealing with hierarchical data, where pieces of data are variously ‘contained in’ or ‘belonging to’ others. Data like this are examples of a general structure called a tree.

Formally, trees are made up of nodes. Each node may have some number of child nodes, and usually one parent node. There is exactly one node in a tree which has no parent, this is the tree’s root node. Nodes which share a parent are sibling nodes, and nodes with no children are leaf nodes.

For many kinds of hierarchical data, we can model its structure as a tree:

Data	Nodes	Root node	\(x\) is a child node of \(y\)
A file system	Files and folders	The root or home directory	\(x\) is in folder \(y\)
Jobs in a company	Employees	CEO	\(x\) reports to \(y\)
Evolutionary tree of life	Species	Some unknown early micro-organism	\(x\) evolved from \(y\)
JSON	Data	The outermost object or array	\(x\) is a member of array or object \(y\)

Interestingly, a family tree is not an example of this kind of tree, as each child typically does not have just one unique parent.

We will generally draw trees with the root node at the top, and all child nodes arranged below, with a line connecting each child to its parent. For instance, in the following tree, the node labelled \(a\) is the root node, and is a parent of \(b\), \(c\) and \(d\) - its children.

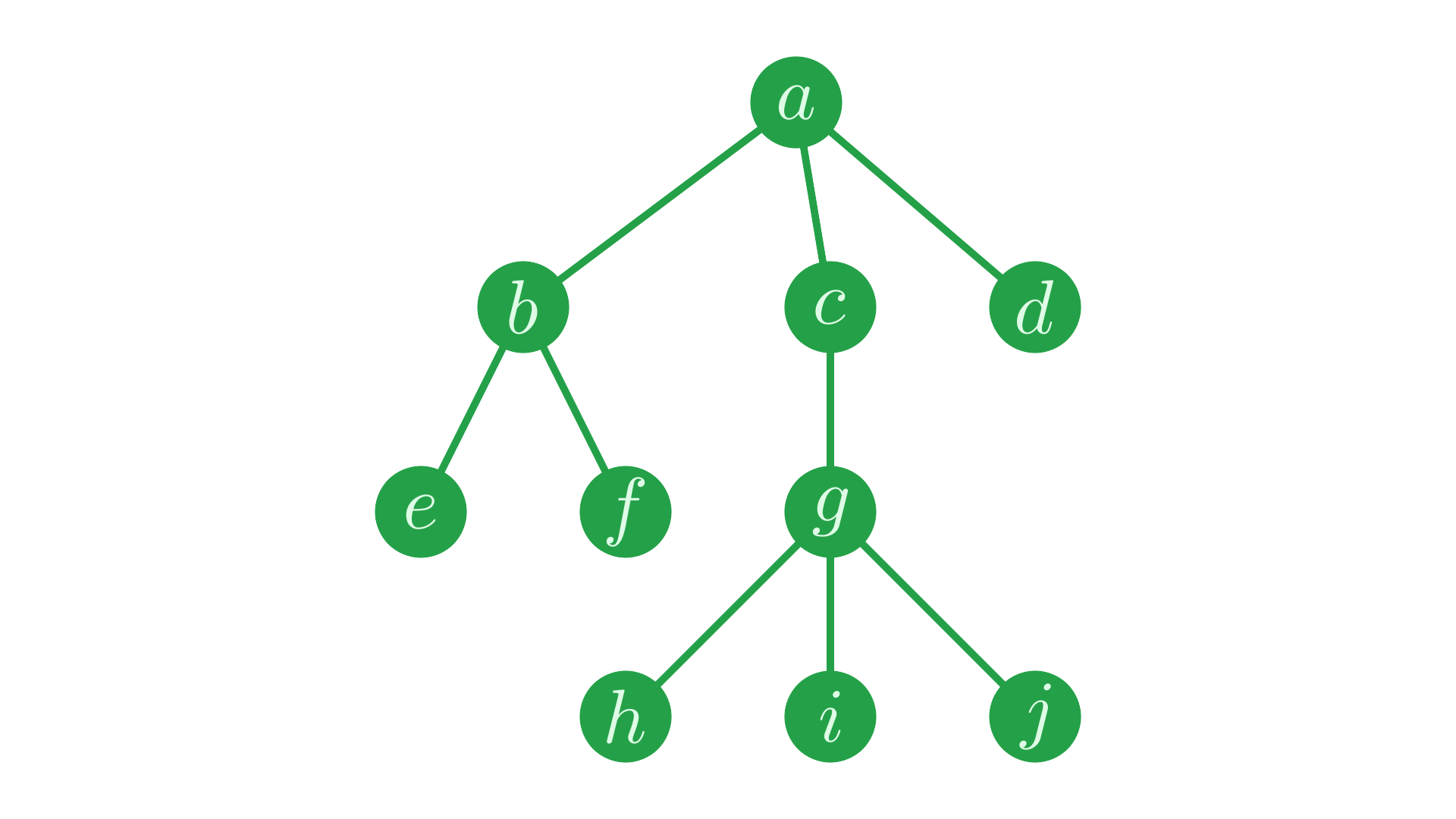
Fig. 1 Baby’s first tree.

So how can we work with trees in APL? The answer, of course, is to find a way to encode the nodes and relationships in an array. In fact, we’re going to find that encoding trees as arrays doesn’t involve bending over backwards to fit a square peg into a round hole - instead we’ll see that the right representation leads to extremely elegant and fast code.

I can take no credit for discovering the techniques discussed in this tutorial. The following resources have been especially influential:

• Aaron Hsu’s thesis on working with tree transformations in the context of a compiler. The thesis is extremely readable, especially for an academic paper, so you’re encouraged to take a look if you’re curious about a specialised application of tree transformation techniques.

• Stevan Apter’s Vector article on working with trees in q, a relative of APL. In various places, you can find trees represented with a parent vector (a technique which we will cover in due course) referred to as ‘Apter trees’ thanks to the influence of this excellent article.

Other useful resources on working with trees in array languages include:

• Devon McCormick’s page on working with trees in J.

• Doug Mennella’s page on drawing trees in J.

• This section of the oK documentation covering two different representations of trees.

• Aaron Hsu’s talks on text processing and tree wrangling.

• Brandon Wilson’s talk on parsing.

• The README of a C++ implementation of Apter trees.